VALUTAZIONE DELL’AZIONE SISMICA CHE ATTIVA I MECCANISMI DI DANNO

1.1. Introduzione

Alla luce degli eventi sismici distruttivi che negli ultimi decenni hanno colpito il territorio italiano, si manifesta sempre più crescente l’interesse per gli studi di vulnerabilità ambientale, e in particolare di vulnerabilità sismica, del patrimonio edilizio storico.

L’attenzione è rivolta soprattutto a quelle tipologie di danni ricor­renti in edifici in muratura osservabili in scenari post-sismici e dovuti a collassi parziali per perdita di equilibrio di pareti o porzioni di pare­ti. Tali collassi sono in genere riferiti sia a pareti investite ortogonal­mente al proprio piano medio (out-of-plane) che ad effetti di azioni si-smiche agenti nel piano delle pareti stesse (in plane).

Gli approcci in analisi limite dell’equilibrio sono molto numerosi nella letteratura recente, in quanto riconosciuti tra i più idonei a rap­presentare il comportamento di questi sistemi murari, soprattutto se­condo la metodologia cinematica. Le pareti murarie sono generalmen­te modellate come insiemi di micro blocchi rigidi con giunti monolate-ri ed attriti vi e l’analisi è rivolta alla valutazione delle azioni sismiche che attivano meccanismi di danno nel piano e fuori dal piano, in fun­zione della geometria delle pareti, dei rapporti dimensionali dei bloc­chi e del coefficiente d’attrito [Livesley 1978, Begg e Fishwick 1995, Casapulla 1999, Baggio e Trovalusci 2000, Casapulla 2001, Ferris e Tin-Loi 2001, Gilbert et al. 2003, Jossa 2005, Orduna e Louren9o 2005, Gilbert et al. 2006]. Particolarmente significative sono le mo-dellazioni di pareti murarie come assemblaggi di macro blocchi rigidi invece che di micro blocchi, con o senza giunti attritivi [Lagomarsino 1998, Casapulla 1999, Azevedo et al. 2000, De Felice e Giannini 2001, Casapulla e Jossa 2002, D’Ayala e Speranza 2003, Lagomarsino e Podestà 2004a, b, Casapulla e Maione 2007]. I diversi studi hanno condotto così alla definizione, talvolta in forma chiusa, dei moltiplica­tori delle azioni orizzontali che attivano i diversi meccanismi analizza­ti, sia nel piano che fuori dal piano. Ciononostante dai confronti tra risultati analitici e risultati sperimentali presenti in letteratura [Restrepo-Vélez e Magenes 2005] emerge che la maggior parte dei moltiplicatori teorici di crisi sono sovrastimati rispetto a quelli reali, sia per mecca­nismi nel piano che per quelli fuori dal piano.

Nel presente lavoro sono esposte le ragioni di questa sovrastima e sulla base di semplici riflessioni viene proposta una nuova procedura di valutazione, orientata a fornire intervalli di soluzioni affidabili.

1.2. Definizione del modello di muratura

Si adotta un modello di muratura a blocchi rigidi con giunti privi di resistenza a trazione ma resistenti per attrito (legge di Coulomb in as­senza di coesione), già opportunamente validato dalla comunità scien­tifica nazionale ed internazionale. L’originalità dei lavori di questa UR sta nel fatto che si rinuncia ad un’analisi discreta con micro blocchi a favore di un sistema articolato in distinti corpi rigidi o macro blocchi separati da un certo numero di lesioni in cui sono assunte concentrate le resistenze attritive. Ciò comporta notevoli semplificazioni, come descritto in seguito.

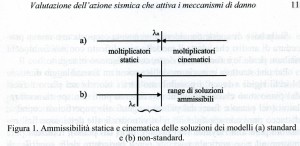
È noto che il modello utilizzato, sia esso con macro o micro bloc­chi, ha un comportamento non standard dovuto a leggi di scorrimento di tipo non-associato. Ciò significa, in pratica, che i classici teoremi dell’analisi limite non garantiscono l’unicità della soluzione in termini di moltiplicatore di crisi, in quanto esiste un range di soluzioni che ri­sultano sia staticamente ammissibili che cinematicamente sufficienti, come illustrato in Figura 1.

In particolare in Figura l(a) è rappresentata la soluzione unica À,_u relativa al modello standard con attrito e dilatanza e in Figura l(b) il range di soluzioni relativo al modello non-standard in assenza di dila­tanza. È noto che la soluzione del primo modello è più grande di quel­la “esatta” relativa al modello non-standard [Drucker 1954, Livesley 1978], ma la definizione di quest’ultima è ancora un problema aperto dal punto di vista computazionale.

In generale, però, se si adotta il teorema cinematico per il modello non-standard, ammesso che si riescano a valutare tutti i cinematismi possibili di una struttura muraria, si ottiene un moltiplicatore A,_c che, essendo il più piccolo del range in Figura l(b), rappresenta una solu­zione a favore di sicurezza e con buona probabilità la soluzione “esat­ta”. Se ne deduce pertanto che la sovrastima sopra introdotta dei mol­tiplicatori cinematici teorici rispetto a quelli sperimentali non è pro­pria del modello adottato ma è da ricercare in altri aspetti della model-lazione.

La ragione di questa sovrastima sta nel fatto che le diverse proce­dure numeriche, sviluppate con approcci cinematici, portano general­mente in conto tutte le massime resistenze attritive che possono gene­rarsi lungo le lesioni. In realtà la resistenza globale è più piccola di quella massima calcolabile, in quanto l’attivazione o meno delle resi­stenze attritive sulle singole superfìci di contatto fra i blocchi dipende dal tipo di meccanismo che si prende in considerazione. Infatti è pre­vedibile, ad esempio, che nel meccanismo di solo scorrimento le resi­stenze attritive si attivino su tutte le superfìci, mentre in quello combi­nato scorrimento-rotazione, sia nel piano che fuori dal piano, non è fa­cile una stima di quali e quante superfìci di contatto attraversate dalla lesione sono effettivamente interessate dallo scorrimento.

Pertanto la ragione della suddetta sovrastima consiste nel passaggio di scala dal modello con micro blocchi a quello con macro blocchi, nel quale si perdono informazioni relative alle superfìci di contatto in cui effettivamente si attiva lo scorrimento.

Sulla base di queste considerazioni è stata proposta una nuova pro­cedura di analisi che adotta il modello semplificato con macro blocchi ma non perde le informazioni dette, come discusso in seguito.

Per una struttura muraria modellata come un assemblaggio di micro blocchi rigidi a secco, i possibili moti tra i blocchi nel piano e fuori dal piano sono classificabili in: scorrimento puro con spostamenti re­lativi (nel piano e fuori dal piano) tangenti alle superfìci di contatto; distacco puro con spostamenti relativi normali alle dette superfìci; ro­tazioni pure alla Heyman (nel piano e fuori dal piano), rotazioni pure intorno ad asse verticale passante per il baricentro delle superfìci di contatto; moti combinati.

Al fine di semplificare l’analisi si assume che i possibili meccani­smi di danno siano caratterizzati da un certo numero di lesioni che se­parano la struttura in distinti corpi rigidi o macro blocchi, lungo le quali si concentrano questi possibili moti relativi tra i micro blocchi. Ad ogni tipo di meccanismo corrisponde un valore della massima e della minima resistenza attritiva (nulla) che si sviluppa lungo la gene­rica lesione. Ha senso quindi definire un dominio di resistenza della lesione, con riferimento solo al tipo di spostamento relativo lungo una lesione, qualunque sia il meccanismo di danno in esame.

Su questi assunti si basa la nuova procedura di valutazione.

Tratto da: “Meccanismi Locali” di Claudia Casapulla

Continua 1/10